2.1 HD-MINTEQ

Simulations were run using the Husby Dynamic MINTEQ model (HD-MINTEQ), which connects the equilibrium calculations of Visual MINTEQ version 3.1 (Gustafsson, 2018); the simple mass balance model (Sverdrup and De Vries, 1994); and the PROFILE model for soil chemical weathering (Sverdrup and Warfvinge, 1993). The details of HD-MINTEQ have previously been described by Löfgren et al. (2017) and in a companion paper by Gustafsson et al. (2018). In brief, it relies on the Stockholm Humic Model (SHM) for organic complexation (Gustafsson, 2001; Gustafsson and Kleja, 2005). The model assumes that the equilibria for ferrihydrite and Al(OH)₃ provide the upper limit for the solubility of Fe³⁺ and Al³⁺ in mineral soil horizons. Further, it uses an extended Freundlich model to simulate SO₄ adsorption (Gustafsson et al., 2015). HD-MINTEQ does not simulate N chemistry; instead dissolved ${\mathrm{NH}}_{\mathrm{4}}^{+}$ and ${\mathrm{NO}}_{\mathrm{3}}^{-}$ in the different horizons are given as input data and are held constant (Table 1). The soil pools of organic C and geochemically active Al were assumed to be constant over the simulated time period. To deal with water transport, HD-MINTEQ uses a 1-D advective–dispersive equation, although the actual dispersion is often governed by the thickness of the modelled soil layers. Vertical flow is assumed, which should be a reasonable approximation for the studied soils, as they were located in recharge areas where the soil surface was nearly flat. The plant uptake is distributed over the two or three uppermost layers, as in the SAFE model of Warfvinge et al. (1993).

Table 1Parameter values and assumptions used for the HD-MINTEQ simulations of all three sites.

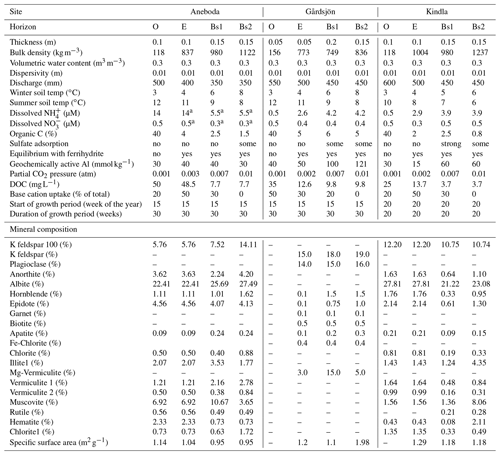
^a These values were adjusted for calibration to account for elevated N concentrations detected in lysimeter data from 2011 onwards. This was due to storm damage (Gudrun) in
the region, which brought down many trees in 2005.

Download Print Version | Download XLSX

2.2 Model setup

In the current application of the HD-MINTEQ model, the soils were compartmentalized into four different discrete horizons: an organic horizon (O), an eluvial layer (E), and two illuvial subsoil horizons (B1 and B2). Simulations were run over a 200-year period from 1880 to 2080, with a 1-week time step. Three different forest stands were simulated – Aneboda (57^∘05^′ N 12^∘32^′ E), Gårdsjön (58^∘40^′ N 12^∘30^′ E), and Kindla (59^∘05^′ N 12^∘01^′ E) (Fig. S1 in the Supplement) – under three different harvest scenarios:

1. conventional harvest (stem-only removal),

2. whole-tree harvest (100 % removal of above-ground logging residues), and

3. no-harvest control (NH).

At all three cites, the harvest events occurred in the year 2020.

The input data for each site and soil horizon are presented in Table 1 and were based on climate and soil profile (Podzol) data collected in earlier work. For the most part, these are given in Löfgren et al. (2011). The bulk densities were estimated as a function of organic C and soil depth using the empirical relationships of Nilsson and Lundin (2006). The volumetric water content was set to a common value of 0.3 m³ m⁻³. The extent of sulfate adsorption in the B1 horizon of Kindla was assumed to be strongly sorbing (“strong” in Table 1), similar to that of another Podzol in the same area of Sweden (Gustafsson et al., 2015). The other two soils from south-western Sweden were assumed to have less (Table 1) sulfate adsorption, in agreement with other soils from this area (Karltun, 1995); the relevant Freundlich parameters were taken from the Tärnsjö soil of Gustafsson et al. (2015). The mineral soil horizons were assumed to be in equilibrium with ferrihydrite, whereas Fe(III) was assumed to be negligible in the O horizons. Dissolved organic C (DOC) was assumed to be constant throughout the simulation period, and the values were calculated from the mean DOC concentrations in soil solution (lysimeter data) between 1993 and 2014.

2.3 Deposition

Historical wet deposition data for the three sites (Fig. S2) were taken from Löfgren et al. (2011) and from Zetterberg et al. (2014). To calculate the contribution from dry deposition, results from measurements of a surrogate surface were used (Ferm and Hultberg, 1995, 1999). Reductions of the total deposition as a result of harvesting were considered using functions of Zetterberg et al. (2014). CH and WTH scenarios used the same deposition profiles, represented by the dotted lines in Fig. S2. In the NH scenario, deposition values were maintained at 2019 levels from 2020 through 2080. The relatively high levels of Na and Cl deposition at Gårdsjön were due to its proximity to the sea. The dips in deposition at Gårdsjön in the early 1900s and Kindla around 1890 were due to historical harvesting events. The dips that occur in 2020 were due to the simulated harvest scenarios. Following the rise and fall of SO₄ throughout the 20th century (grey shaded and labelled “historical acidification”) at all three sites, the influence of industrial emissions and subsequent regulations can be clearly seen. Currently, the SO₄ deposition is similar to the levels observed in the 1930s.

2.4 Plant uptake

BC uptake trends at Kindla and Aneboda (Fig. S3) were calculated as described previously (Zetterberg et al., 2014). Briefly, biomass at any given time point was used to allocate the cation amount over time according to classical growth curves and information regarding any natural event (e.g. storms and fire) or silvicultural measures (e.g. clear-cutting and thinning) that have taken place during the rotation period. The final uptake curves were created by multiplying the biomass increments by the nutrient concentrations for various tree parts. BC uptake rates are based on current biomass (hindcast scenario) and future biomass predictions by the Swedish forest growth model ProdMod, version 2.2 (Ekö, 1985). BC uptake values were finally corrected for litterfall (which returns BCs to the soil) and remineralization estimates. The net BC uptake at Gårdsjön was estimated using the ForSAFE model, by dynamically simulating photosynthesis, growth, and gross uptake in response to environmental drivers and subtracting litterfall that was physiologically simulated in response to light saturation, respiration, and water availability (Belyazid and Moldan, 2009).

The highest rates of net uptake occur in young growing forests, and as the forest stands age, less BCs are taken up. The stack of graphs in the left column of Fig. S3 represents the NH scenario, which means that for Aneboda and Kindla, uptake trends after 2019 were modelled using an exponential decay and essentially approach zero as time goes on. The stack of graphs in the central and right columns (Fig. S3) represents the uptake trends that were used from 2020 and onwards under the CH and WTH scenarios, respectively. The negative values in uptake that occur after harvesting events are due to net influx of BCs originating from mineralization of leftover debris. The CH scenarios produce more negative values than WTH scenarios because there is more debris left on the soil. It should also be noted that the assumed 100 % removal of harvest residuals in the WTH scenario is an overestimation; in practice, ∼70 % is removed (Nilsson et al., 2015).

2.5 Mineralogy and weathering

For Aneboda and Kindla, the mineralogy used in the PROFILE submodel was calculated from data on total elemental analysis using the A2M model (Posch and Kurz, 2007). For Gårdsjön, the mineralogy was taken directly from Martinson et al. (2003). The specific surface area used by PROFILE was estimated from the particle-size distribution using the relationship of Sverdrup (1996). The mineralogy data are presented in Table 1. To calculate weathering rates, the relationships of Sverdrup and Warfvinge (1993) were used. The only modification in the current work was the way in which the organic anion concentrations [R⁻] (mol L⁻¹) were calculated, as HD-MINTEQ uses the SHM, whereas the original PROFILE model used the Oliver equation. Thus, the main equation to calculate the weathering rate is

where r is the weathering rate ($\mathrm{keq}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) for an individual mineral; $k_{{\mathrm{H}}^{+}}$, $k_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, and k_R are the rate coefficients for the reaction with H⁺, H₂O, and DOC, respectively (m s⁻¹); n_H, $n_{{\mathrm{CO}}_{\mathrm{2}}}$, and n_R are the reaction orders of individual reactions; $P_{{\mathrm{CO}}_{\mathrm{2}}}$ is the partial CO₂ pressure (atm); and f_H, $f_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, and f_R are the retardation factors (“brakes”). The latter are defined as

where k_Al, k_BC, and k_R are saturation coefficients for dissolution reductions, whereas x_Al, x_BC, z_Al, and z_BC are reaction orders. Values of all coefficients and reaction orders were taken from Sverdrup and Warfvinge (1993).

2.6 Calibration

To initialize the model, dissolved concentrations of major cations, anions, and DOC were provided for the first time step (in 1880) and for the solid-phase geochemically active Al (Table 1). Based on this input, HD-MINTEQ then calculated the start pH and the corresponding sorbed concentrations of major ions as well as dissolved Al.

The model was calibrated in an iterative process in which geochemically active Al and the plant uptake percentages of the different layers were adjusted. Further, it was assumed that the soil water chemistry was in a steady state with respect to the environmental conditions in 1880, i.e. with respect to the assumed values for atmospheric deposition, plant uptake, weathering, etc. Before calibration, an initial guess was made of geochemically active Al and of the base cation uptake percentages. During each iteration, the first step was to run the model for 1000 years with the 1880 parameters to obtain initial (start-state) values of dissolved ions. Final values produced after a 1000-year simulation were then used to initiate the model, which was rerun with historical disturbances and changes in atmospheric deposition. The modelled values of pH, dissolved inorganic Al, and other BC concentrations from 1993 to 2014 were then compared to soil solution data from the same period taken from various depths and binned into either horizon E or B before being plotted (Löfgren et al., 2011). Further, it was checked that the assumed BC uptake percentages did not result in uneven depletion rates in the different layers; if so, the percentages were adjusted. Based on the above, refined guesses of geochemically active Al and of the plant uptake distribution could be made for the next iteration.

During the initial model runs, it was found that the modelled drop in pH after 2020 at Aneboda and Kindla was limited by the amount of sorbed Ca²⁺, restricting Ca²⁺ available for vegetation uptake. In the harvesting scenarios the sorbed Ca²⁺ pool was not replenished in spite of the increased pH after historic acidification, which is similar to what was observed in the MAGIC simulations of Zetterberg et al. (2014). This in turn led to extremely low levels of dissolved Ca²⁺ and to occasional model errors due to negative concentrations in preliminary model runs. To stop this from happening, the net Ca²⁺ uptake was decreased as dissolved Ca²⁺ decreased, according to the following relationships taken from the “old” SAFE model (Alveteg, unpublished):

where Ca_upt,real is the adjusted net Ca uptake, Ca_upt,init is the assumed Ca uptake according to Table 1, and f_upt is defined by

where n=4 and $c=\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{6}}$. These equations prevented dissolved Ca²⁺ concentrations from falling below 5 µmol L⁻¹, but they also limited the acidification effect due to Ca uptake. To what extent trees will adjust their BC uptake in response to lower availability in the soil is still debated (Zetterberg et al., 2014). In plot experiments in which the effects of harvesting were studied, the depletion of sorbed Ca²⁺ was less severe than that predicted by mass balance calculations and models (Zetterberg et al., 2014). Possible reasons include both a lower Ca²⁺ uptake to trees and mineralization of strongly bound Ca²⁺ in litter, which is otherwise not geochemically active. However, because the HD-MINTEQ simulations here produced stronger effects on soil Ca compared to those observed in the field (Zetterberg et al., 2016), it seems probable that the acidification effect as predicted by HD-MINTEQ may be regarded as a worst-case scenario and that the real acidification, at least over the first rotation period, may be even smaller. However, at this point it needs to be added that these conclusions may not be relevant in cases when nitrification following harvest is substantial, in which case the acidification effect could be considerably larger; this possibility was not considered in our simulations. Most Swedish forests are N limited (Högberg et al., 2017), but increased nitrate concentrations are found in soil solution for some years after final felling. Nitrification is dependent on site productivity, which is between 4 and 8 ${\mathrm{m}}^{\mathrm{3}}{\mathrm{ha}}^{-\mathrm{1}}{\mathrm{yr}}^{-\mathrm{1}}$ in the sites studied. According to the estimates of Futter et al. (2010), the total accumulated harvest effect should generally not exceed 220 and 500 $\mathrm{meq}{\mathrm{NO}}_{\mathrm{3}}^{-}{\mathrm{m}}^{-\mathrm{2}}$ for site productivities of 4 and 8 ${\mathrm{m}}^{\mathrm{3}}{\mathrm{ha}}^{-\mathrm{1}}{\mathrm{yr}}^{-\mathrm{1}}$, respectively (Futter et al., 2010), indicating rather modest nitrification effects on the long-term acid–base status of the soils. As an example, this value represents between 5 % and 15 % of the atmospherically deposited BCs over a full rotation period; hence nitrification is a relatively minor proton source as compared to other processes in the forest soils under study.

3.1 Historic acidification

Historic acidification of forest soils from atmospheric deposition of S took place from 1940 through 2000 and can be seen in the modelled soil solution pH profiles at Aneboda (Fig. 1a), Gårdsjön (Fig. 2a), and Kindla (Fig. 3a). At Aneboda, the lowest soil solution pH for each horizon occurred around 1990, about the same time that atmospheric S deposition began to decline (Fig. S2). The most dramatic decrease in pH at Aneboda occurred within the B1 horizon, dropping from pH 5.29 in 1940 to pH 4.81 in the late 1980s, a total pH decline of 0.48 units in 47 years. The other horizons (O, E, and B2) at Aneboda saw milder changes in pH (<0.20 units) over the same time period. The effects of historical acid rain can also be seen in the BC profiles of Ca²⁺ and Mg²⁺, most significantly in the B1 and B2 horizons of Aneboda. An increase in dissolved BCs occurred in order to balance the charge created by increasing levels of anions (${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ and ${\mathrm{NO}}_{\mathrm{3}}^{-}$) being deposited from the atmosphere; i.e. these BCs were exchangeable and responsive to anion concentrations. Between 1940 and 1980, dissolved Ca²⁺ concentrations increased by 275 % and 94 % in the B1 and B2 horizon, respectively. The anomalous blip in pH (and BCs) at Aneboda occurring between 2008 and 2018 is the result of a large storm that downed many trees in 2005, followed by a bark beetle infestation, resulting in mineralization, acidification, and increased dissolved Ca²⁺ (Löfgren et al., 2014).

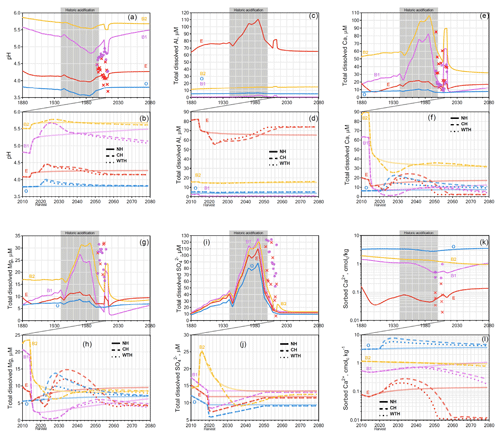
Figure 1Graphs for Aneboda. Simulated mean annual pH (a, b); total dissolved Al (c, d), Ca (e, f), Mg (g, h), and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ (i, j); and sorbed Ca²⁺ (k, l). Chemical dynamics in response to historic acidification (a, c, e, g, i, k) are presented above the response to harvesting events (b, d, f, h, j, l). The solid, dashed, and dotted lines represent the annual averages in the NH, CH, and WTH scenarios, respectively. The grey box spanning 1940 to 2000 represents the period of acidification due to S deposition. The symbols “×” and “•” represent the annual averages of empirical measurements in the E and B horizons, respectively.

Download

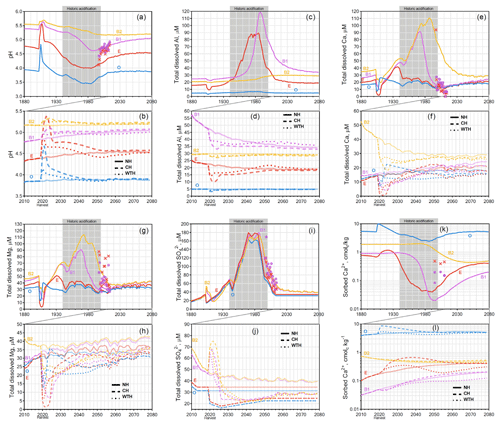
Figure 2Graphs for Gårdsjön. Simulated mean annual pH (a, b); total dissolved Al (c, d), Ca (e, f), Mg (g, h), and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ (i, j); and sorbed Ca²⁺ (k, l). Chemical dynamics in response to historic acidification (a, c, e, g, i, k) are presented above the response to harvesting events (b, d, f, h, j, l). The solid, dashed, and dotted lines represent the annual averages in the NH, CH, and WTH scenarios, respectively. The grey box spanning 1940 to 2000 represents the period of acidification due to S deposition. The symbols “×” and “•” represent the annual averages of empirical measurements in the E and B horizons, respectively.

Download

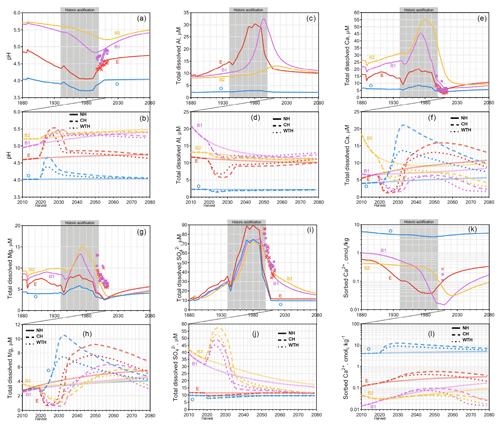
Figure 3Graphs for Kindla. Simulated mean annual pH (a, b); total dissolved Al (c, d), Ca (e, f), Mg (g, h), and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ (i, j); and sorbed Ca²⁺ (k, l). Chemical dynamics in response to historic acidification (a, c, e, g, i, k) are presented above the response to harvesting events (b, d, f, h, j, l). The solid, dashed, and dotted lines represent the annual averages in the NH, CH, and WTH scenarios, respectively. The grey box spanning 1940 to 2000 represents the period of acidification due to S deposition. The symbols “×” and “•” represent the annual averages of empirical measurements in the E and B horizons, respectively.

Download

Of the three sites studied, the strongest effect of historic acid rain was seen at Gårdsjön (Fig. 2a), which experienced an average decline of 0.39 pH units across all four horizons. This is likely due to the higher S (as sulfuric acid) deposition at Gårdsjön (Fig. S2). The horizon subject to the most drastic acidification was the E horizon, which experienced a sharp decline from pH 4.81 in 1940 to pH 4.02 by 1985 (a drop of 0.70 pH units in 45 years). Similar to Aneboda, Gårdsjön experienced its most acidic soil conditions in the mid 1980s. However, the B1 horizon did see a slight delay, experiencing its most acidic conditions in the early 1990s. This trend in delayed acidification across horizons was even more pronounced at Kindla (Fig. 3a), where the O and E horizons reached their most acidic conditions by 1980, the B1 horizon continued to acidify until 1994, and the B2 horizon did not reach its most acidic conditions until 2013 (nearly 25 years after the S and N deposition began to decline, Fig. S2). The delayed response was mainly attributed to SO₄ adsorption and desorption, which is known to delay response times to decades for strongly SO₄-adsorbing soil systems (Cosby et al., 1986).

The dissolved aluminium profiles at all three sites show that most of the mobilization of dissolved Al occurred in the E horizon. This was likely due to the higher pH of the B horizons (pH>5), where the precipitation of aluminium hydroxide and/or allophane removed soluble Al (Gustafsson et al., 1995; Karltun et al., 2000). This inverse relationship with pH is demonstrated clearly for Kindla's B1 horizon, where soluble Al concentration peaked as pH decreased below 5 (Fig. 3). The low levels of soluble Al in the O horizon are attributed to complexation with organic ligands.

For the Gårdsjön and Kindla sites, the modelled results align well with the lysimeter data, with a few exceptions. Interestingly, the model underestimated Mg²⁺ concentrations at both sites. This could be caused by the use of A2M estimates, i.e. that the normalization model underestimated the presence of easily weathered Mg-containing minerals. In a recent study, Casetou-Gustafson et al. (2018) compared A2M with the mineralogy obtained by X-ray powder diffraction (XRPD) for two soils that were similar to the soils studied here. They found that trioctahedral mica and hydrobiotite were consistently underestimated by A2M, which is consistent with our modelling results as these Mg-containing minerals have relatively high weathering rates. Moreover at Kindla, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ concentrations were underestimated. There may be several explanations, but one possibility is mineralization and oxidation of organically bound S (Löfgren et al., 2001, 2014). The delay in ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ decrease at Kindla was, however, predicted well in the B1 horizon of the model.

For the Aneboda site, the discrepancies between model and observations were more substantial. For example, while ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ and pH were grossly underestimated, Ca²⁺ and Mg²⁺ were overestimated. It is important to note that the lysimeter data plotted in Figs. 1, 2, and 3 are averages based on data from several lysimeters, and it has previously been observed that there are large variations in the results of individual lysimeters at the Aneboda site (Löfgren et al., 2010, 2011, 2014). As an example, for the B horizon the averaged results are based on eight lysimeters. Three of these, nos. 7102, 7104, and 7105, had results that were clearly divergent from the others (Fig. S4). Dissolved ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, Ca²⁺, and Mg²⁺ were all considerably higher, whereas the pH was lower. Possible reasons include a net mineralization and oxidation of organically bound sulfur in response to decreased S deposition (Löfgren et al., 2001, 2014), a process which was not taken into account in the model. It may also be observed that if the results from the three lysimeters were removed, there would be a clearly improved agreement between the model and the observations.

3.2 Harvesting-induced acidification

One trend across all horizons at all sites was that, directly after a simulated harvesting event (CH or WTH) in 2020, the pH sharply increased for 5–10 years before slowly declining over the remainder of the simulation (displayed in Figs. 3b, 4b, and 5b). The increase in pH immediately following a harvest event is primarily caused by mineralization of BC-containing harvest residues (Fig. S3), but also marginally by a decreased dry S deposition. These processes increase the sorption of BCs on the exchange sites (Figs. 1l, 2l, and 3l). The impact of harvesting on pH and sorbed Ca lasted for three to four decades at all three sites, eventually converging towards the NH scenario, before falling below it, which was demonstrated previously in long-term experiments (Zetterberg et al., 2016). However, once new stands have been established and trees begin to grow, uptake drives a net loss of BCs from the soil, leading to acidification. Across all three sites, the B1 horizons became the most acidified by 2080 compared to the NH scenario. The O horizon experienced the least change after harvesting events, and at Aneboda and Kindla the pH was slightly more basic compared to the NH scenario by 2080. However, had the simulation been run for a longer time, it appears that the pH would eventually reach NH levels or drop below them. In reality a second harvest would likely have occurred after some 80–100 years, yielding a new period with a brief pH increase.

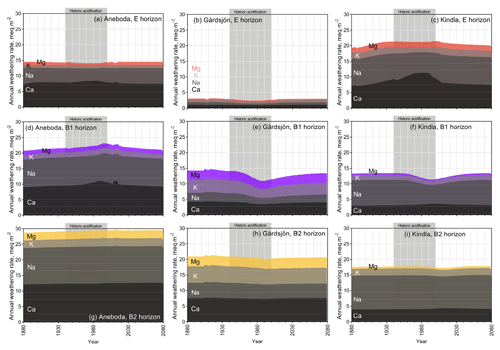
Figure 4Stack plot of simulated base cation weathering rates in the NH scenario, with subdivisions of elemental components.

Download

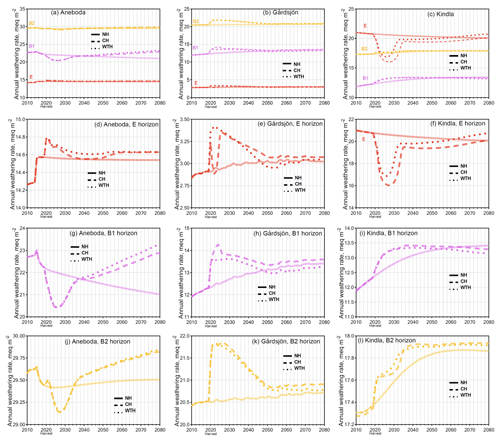
Figure 5Simulated effects on base cation weathering rates in the conventional harvest (CH), whole-tree harvest (WTH), and NH scenarios. The time series starts in 2010 just before harvest and the graphs are scaled in order to demonstrate differences between harvest intensities at the different sites and soil horizons.

Download

Comparing the two harvesting scenarios demonstrates that over the 60-year time frame studied, simulated WTH acidified the soil more than CH, but not by much even though 100 % of the harvest residues are assumed withdrawn at WTH. At Aneboda, the pH across all horizons dropped by an average 0.13 (WTH) and 0.12 units (CH) compared to the NH scenario by the year 2080. The difference between WTH and CH was more pronounced at Kindla, which saw a mean pH decrease across all horizons of 0.10 (WTH) and 0.04 (CH) units compared to the NH scenario by 2080. The most sensitive horizon to harvesting at Aneboda was the B1 horizon, which dropped in pH by 0.42 (WTH) and 0.36 (CH) units compared to the NH scenario by the year 2080. Aneboda's B1 horizon also experienced a significant loss of soluble Ca²⁺ after harvesting, decreasing by 65 % (WTH) and 56 % (CH) by 2080 compared to the NH control. However, on a percentage basis, Aneboda's E horizon experienced the most precipitous loss of soluble Ca²⁺ after harvesting, decreasing by 87 % (WTH) and 86 % (CH) by 2080 compared to the NH control. Similar trends were seen in sorbed Ca²⁺ concentrations at Aneboda by 2080. The E horizon experienced a 92 % (WTH) and 91 % (CH) decrease compared to the NH control, while the same figures for the B1 horizon were 83 % and 75 %, respectively. Neither harvesting scenario appeared to have a tangible impact on the Ca²⁺ concentrations (soluble or sorbed) in the B2 horizon at Aneboda. Contrary to the trends in Ca²⁺ concentrations in horizons E, B1, and B2, after harvesting, the O horizon experienced an increase in soluble and sorbed Ca²⁺ by 2080 compared to the NH control.

Compared with the NH scenario, Kindla also experienced a phase with an increased pH followed by acidification at the end of the simulation period, but to a lesser degree than Aneboda. At Kindla, the mean soil pH at 2080 decreased by an average of 0.04 and 0.10 units after CH and WTH, respectively. The B1 horizon was the most sensitive to acidification in both harvesting scenarios. Of the Kindla horizons, B1 also saw the greatest change in soluble and sorbed Ca²⁺ after harvesting. Soluble Ca²⁺ decreased by 80 % (WTH) and 73 % (CH), while sorbed Ca²⁺ decreased 91 % (WTH) and 84 % (CH) by 2080 compared to the NH scenario. One interesting observation at Kindla was that the delayed acidification with increasing soil depth, which was related to ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ adsorption and desorption processes and historic acidification, was not observed after harvesting. Our simulations indicate that biological acidification did not initiate such processes, at least within 60 years after harvest, corresponding to an almost full rotation period.

A pH increase after harvesting was also observed at Gårdsjön, with the O and E horizons experiencing the strongest response. After increasing for a couple of years after harvest, the pH started to decline, slowly approaching the NH trend line. By the end of the simulation (2080), there was almost no difference between CH, WTH, and the NH scenarios, and, contrary to the trends at Aneboda and Kindla, it did not appear that the soils were trending towards further acidification post-2080. This trend of disturbance immediately following a harvest before slowly approaching the NH trends can also be seen in BC concentrations. Total dissolved Al, Ca, and Mg sharply decreased immediately after CH and WTH for several years before meandering towards the NH trend line. However, by 2080, the concentration of soluble BCs after WTH was significantly lower than after CH, and both harvesting events resulted in less soluble BCs compared to the NH scenario. Exchangeable Ca²⁺ concentrations following harvesting events at Gårdsjön appeared to oscillate around the NH trend line: increasing immediately after harvest (similar to Aneboda and Kindla), before slowly decreasing (also similar to Aneboda and Kindla), but then again increasing to approach the NH levels of sorbed Ca²⁺. There are several possible explanations for the Ca²⁺ profiles at Gårdsjön. First, Gårdsjön has a relatively high organic carbon content (Table 1), which governs the cation exchange capacity, resulting in higher exchangeable Ca²⁺ to buffer the soil pore water. Also, atmospheric deposition at Gårdsjön is significantly higher than at the other locations (Fig. S2), resulting in a higher-ionic-strength pore water, which would result in quicker transport of soluble ions between the horizons.

The absolute magnitude of the model-predicted changes is of course uncertain, not least in the light of the mixed success of the model to predict the available lysimeter data, as discussed in the previous section. Nevertheless, the simulated results strongly suggest that the acidification due to a harvesting event in 2020 would be less impactful, over the time range studied, than that of historic atmospheric acidification. Even though the pH in the WTH and CH scenario decreased with time as compared to the NH scenario, the simulated pH did not drop to the levels observed around the peak of historic acidification (1980–1990). As was discussed by Löfgren et al. (2017), this reflects the different acidification mechanisms involved. Most importantly, the concentration of mobile anions was much lower in the harvesting scenarios compared to the levels around the 1980s and 1990s, and this limits the potential pH decrease.

3.3 Weathering and release of base cations

The weathering rates as calculated by the PROFILE submodel in HD-MINTEQ differed across locations and layers in response to historic acidification and the presence of weathering brakes such as Ca²⁺ and Al³⁺ (Eqs. 2 and 3). Across all sites and layers, the major BCs released by weathering were Ca²⁺ and Na⁺ (Fig. 4). During the historic acidification period, the annual weathering rates at several sites and horizons (Aneboda: E; Gårdsjön: E, B1, and B2; Kindla: B1 and B2) actually decreased (Fig. S5), although not by much. This is due to the brakes in the weathering function (i.e. from Al³⁺ and BCs, Eqs. 2 and 3) and to the fact that total dissolved Al and BCs were much higher during this period (Figs. 1, 2, and 3). In other words, the increased weathering rate expected from a decreased pH was offset by the increase in dissolved Al and BCs, resulting in a very small net effect, which according to PROFILE was negative. However, the exact patterns varied from site to site and from layer to layer. The low weathering rates in the E horizon at Gårdsjön were likely due to its mineralogy; i.e. minerals other than quartz, K feldspar, and plagioclase were essentially absent from the E horizon, but they were present further down in the profile. Another factor leading to low weathering rates in the Gårdsjön E horizon was the relatively thin layer thickness.

Contrary to the decrease in weathering rates during the historic acidification of the 1970s, the simulated weathering rates after the harvesting scenarios in 2020 generally increased compared to NH by 2080 (Fig. 5) although, again, the net change was very small. However, the dynamics were quite different across each layer and site. The B1 horizon at Aneboda saw the strongest increase in weathering rates after harvesting, increasing by 9 % (CH) and 11 % (WTH) by 2080 compared to the NH scenario. The other horizons at Aneboda (E and B2) had almost unchanged weathering rates (<2 % increase by 2080 compared to a NH scenario). It is worth noting that the difference between harvesting events and NH at the Aneboda B1 and B2 horizons would likely continue to diverge beyond 2080. At Aneboda, by the year 2080, the sums of weathered BCs for the CH and WTH scenarios were 32 meq m⁻² (CH) and 46 meq m⁻² (WTH) higher, respectively, than the BCs weathered in the NH scenario (Fig. S6). To put this into perspective, this difference is equivalent to only 1.1 % and 1.7 %, respectively, of the atmospherically deposited BCs in the WTH plots over the same period. Such a small change in the weathering rate cannot be experimentally verified and is unlikely to be of any ecological significance.

The trends in simulated weathering rates at Gårdsjön after harvesting mimicked the trends seen in pH; i.e. they rapidly increased for a couple of years, before declining to approach levels similar to the NH scenario. For all three layers at Gårdsjön, the modelled weathering rates appeared to reach steady-state conditions by the year 2055, whereas the weathering rates at Kindla and Aneboda deviated from the NH trend lines well into 2080. On a mass basis, CH and WTH at Gårdsjön resulted in amounts of weathered BCs that were 74 and 49 meq m⁻² higher than in the NH scenario by the year 2080 (Fig. S6). This change is equivalent to 0.6 % and 0.4 %, respectively, of the sum of atmospherically deposited BCs in the WTH plots.

At Kindla, no horizon saw an increase in simulated weathering rate greater than 3.4 % by 2080, compared to the NH scenario. In fact, when weathering of the three mineral soil layers was summed, weathering rates slightly decreased by 0.9 % (CH) and 2.0 % (WTH) by 2080 compared to the NH scenario, which was equivalent to a decreased amount of weathered BCs of 64 and 26 meq m⁻², respectively, over the simulated time period (Fig. S6). This result was influenced mainly by the large decrease in weathering rates in the E horizon in response to the pH increase after harvest (Fig. 3f), and the change is equivalent to 2.0 % and 0.8 % of the atmospherically deposited BCs.

Weathering is dictated by both H⁺ (the lower the pH, the more weathering) and by the weathering brakes in the model, most importantly dissolved Al³⁺ (the more Al³⁺, the less weathering). Some layers followed the generally expected trend of increased weathering rates with lower pH (B1 and B2 of Aneboda, and E of Kindla). These same layers were also low in dissolved Al³⁺ (Fig. S7), so the Al³⁺ weathering brake (the first terms of Eqs. 2 and 3) was not strong, and as a result the H⁺ concentration dictated mineral weathering. In all other layers (E of Aneboda, all horizons in Gårdsjön, and both B horizons of Kindla) the simulated weathering rates decreased with lower pH, which was due to a relatively high concentration of dissolved Al³⁺ that caused the Al³⁺ weathering brake to be important. There is a certain threshold range in the model where the weathering brake due to Al³⁺ concentration started to influence weathering rates greatly, rendering H⁺ concentration less important. The “weathering rate vs. Al” profiles in Fig. S7 show the transition from pH-controlled weathering to Al-controlled weathering – weathering rates increase with increasing Al concentrations until a “break point” Al concentration is reached, where weathering rates begin to level off and decline. There are other weathering brakes as well, such as Ca²⁺, that limit the effect of pH-induced weathering (Eq. 2), but these were less important. Although not obvious at first, the trends in simulated weathering rates within an individual layer were consistent, regardless of the source of acidification (be it acid rain or harvesting).

As mentioned previously, limitations in the model prevented us from addressing possible nitrification effects resulting from long-term N deposition, which may influence these results. A future task is to upgrade the HD-MINTEQ model to include N transformations, so that the effects arising from, for example, N deposition and nitrification can be more accurately assessed. Further, improved estimates of the mineralogical composition through, for example, X-ray diffraction would be desirable to avoid the mismatch in individual base cations, as was observed for Mg²⁺.

Although the model was parameterized for three Swedish forest sites, the main trends are likely to be valid also for forest soils in other parts of the world, i.e. that forest management practices are not likely to result in strong acidification effects within one full rotation period. However, these results should not be extrapolated to longer time perspectives, as certain drivers of the model may be increasingly uncertain with time. For example, it is not known to what extent the base cation uptake behaviour will differ between NH, CH, and WTH scenarios over a period of several rotations.