the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Arable soil formation and erosion: a hillslope-based cosmogenic nuclide study in the United Kingdom
John N. Quinton
Andrew M. Tye
Ángel Rodés
Jessica A. C. Davies
Simon M. Mudd
Timothy A. Quine
Arable soils are critical resources that support multiple ecosystem services. They are frequently threatened, however, by accelerated erosion. Subsequently, policy to ensure their long-term security is an urgent societal priority. Although their long-term security relies upon a balance between the rates of soil loss and formation, there have been few investigations of the formation rates of soils supporting arable agriculture. This paper addresses this knowledge gap by presenting the first isotopically constrained soil formation rates for an arable (Nottinghamshire, UK) and coniferous woodland hillslope (Shropshire, UK). Rates ranged from 0.026 to 0.096 mm yr−1 across the two sites. These rates fall within the range of previously published rates for soils in temperate climates and on sandstone lithologies but significantly differed from those measured in the only other UK-based study. We suggest this is due to the parent material at our sites being more susceptible to weathering. Furthermore, soil formation rates were found to be greatest for aeolian-derived sandstone when compared with fluvially derived lithology raising questions about the extent to which the petrographic composition of the parent material governs rates of soil formation. On the hillslope currently supporting arable agriculture, we utilized cosmogenically derived rates of soil formation and erosion in a first-order lifespan model and found, in a worst-case scenario, that the backslope A horizon could be eroded in 138 years with bedrock exposure occurring in 212 years under the current management regime. These findings represent the first quantitative estimate of cultivated soil lifespans in the UK.
- Article
(913 KB) - Full-text XML
-
Supplement
(481 KB) - BibTeX
- EndNote
Soil erosion is a significant threat to society (Pimentel et al., 1995; UNCCD, 2017). Whilst uncultivated “pristine” soils may develop steady-state thicknesses, where erosion and production are in dynamic equilibrium (Phillips, 2010), human-induced erosion has led to soil thinning across many landscapes (Montgomery, 2007). Soil erosion, left unchecked, can ultimately lead to the removal of the soil cover and the exposure of the underlying parent material (Amundson et al., 2015). The development of soil conservation strategies has long been an active field for research and practice (Panagos et al., 2016; Govers et al., 2017). Given any long-term strategy to preserve soil resources relies upon a balance between the rates of soil loss and soil renewal (Hancock et al., 2015), the measurement of soil formation is a fundamental component in these conservation efforts.
The mechanisms associated with soil formation have been studied for over a century, with a focus on the development of soil horizons and the evolution of soil properties (Dokuchaev, 1879; Jenny, 1941; Bryan and Teakle, 1949; Tugel et al., 2005). Efforts to quantify the rates at which soils form from parent materials have included studying how soil properties change across chronosequences (Turner et al., 2018), developing chemical weathering models (Burke et al., 2007) and, in particular, employing terrestrial cosmogenic radionuclide analyses (Heimsath et al., 1997). In the latter, the concentrations of radioactive isotopes in the bedrock, which are partly dependent upon the rate at which bedrock transforms into soil, are measured and assumed to equal the rates of soil formation.
Despite the recent advancements in cosmogenic radionuclide analysis, their application in soil science has, arguably, not been fully realized. Moreover, there are three research challenges that may explain this. First, there is a dearth of soil formation rate data. Whilst there have been many attempts at calculating a global average soil formation rate from collating multiple inventories (Alexander, 1988; Montgomery, 2007; Stockmann et al., 2014; Minasny et al., 2015), these datasets often omit more than 100 countries, particularly in Africa and Europe, presenting a clear rationale for more studies to take place in these areas of the world. Second, over 80 % of the soil formation rate inventory, comprising data from Montgomery (2007), Portenga and Bierman (2011) and Stockmann et al. (2014), is attributed to samples taken from outcrops and stream sediments procured from drainage basins. Moreover, only 252 10Be-derived rates from this inventory of 1850 stem from samples extracted from underneath the soil mantle. In addition, the majority of these stem from mountain regions and deserts (Heimsath et al., 1997; Wilkinson et al., 2005; Zhao et al., 2018; Struck et al., 2018). This is partly because the observation and estimation of bedrock weathering rates is most commonly carried out by the geomorphological community, principally to identify the mechanisms behind long-term landscape evolution (Heimsath, 2006; Heimsath and Burke, 2013; Ackerer et al., 2016; Zhao et al., 2018). As a result, there has been no investment in deriving rates of soil formation for soils that support arable agriculture (Heimsath, 2014), despite these soils being identified as a societal priority (FAO and ITPS, 2015). Such soils are critical to the delivery of multiple ecosystem services and, for many countries, are one of the most critical resources in ensuring the health of the society and sustained economic growth. They are also often intensely managed and thus the loci for accelerated erosion (Quinton et al., 2010; Borrelli et al., 2017). However, in the absence of soil formation rate data, the magnitude of the threat erosion places on the sustainability of soils and arable production is unknown, amounting to a critical knowledge gap. Third, although the distributions of inventoried soil erosion and formation rates are often presented together to demonstrate the severity of soil erosion (Montgomery, 2007; Minasny et al., 2015), the spread of globally compiled data is such that it cannot offer a useful forecast of the sustainability of soil at a site scale. Both distributions are platykurtic, and there is substantial overlap in these rates: 0–28.8 mm yr−1 for soil formation (Minasny et al., 2015) and 0–52.9 mm yr−1 for soil erosion (Montgomery, 2007). For a greater understanding into the sustainability of soil resources at the local scale, we argue that soil scientists should undertake empirical measurements of both soil formation and erosion in parallel.
In this UK-based study, we present 10Be-derived soil formation rates for two catena sequences in an arable and coniferous woodland setting. The former are the first of their kind globally, and the latter are the first of their kind in Europe. We place our results in the context of the rates previously derived in similar climatic and petrographic settings around the world. Finally, using previously measured soil erosion rates at the arable site, we calculate first-order soil productive lifespans to infer the long-term sustainability of the soil resource.
2.1 Site description
This study measures soil formation down two catena sequences (Fig. 1). The first is an arable hillslope at Rufford Forest Farm (RFF), east of Mansfield in Nottinghamshire, UK (53∘7′13.43′′ N, 1∘4′39.61′′ W). The second is a woodland hillslope in Comer Wood (CW), north of Quatford in Shropshire, UK (52∘30′30.43′′ N, 2∘22′45.68′′ W). RFF was selected as it is the site of previous tillage and water-based erosion studies (Quine and Walling, 1991; Walling and Quine, 1991; Govers et al., 1996). Electing CW as a sister site is justified based on its similarities in parent geology, macroclimate and soil physical properties with RFF as detailed below. A Trimble S6 Total Station was used to measure the relative elevation and slope of the catenas at both sites (Fig. 1b).
A reconnaissance study of the parent materials and their feasibility for cosmogenic radionuclide analysis was undertaken in spring 2017. Both sites are underlain by Triassic sandstone. At RFF, the Sherwood Sandstone (Chester formation; Olenekian, 247–251 Ma) is described as pinkish to red, medium to coarse grained, pebbly, cross-bedded and friable. In CW, the New Red Sandstone (Bridgnorth formation; Cisuralian, 273–299 Ma) is described as brick-red, medium grained, cross-bedded and aeolian based. Both RFF and CW are south-facing slopes, and sit in a temperate oceanic climate (Cfb), between 96–99 and 50–71 m a.s.l., respectively. The mean annual precipitation and temperature is 709 mm and 9.8 ∘C at RFF and 668 mm and 9.9 ∘C in CW, respectively (Met Office, 2018).
Both sites are positioned beyond the areal limits of the Late Devensian ice sheet, but studies conducted on similar formations of Triassic Sherwood Sandstone nearby suggest that the weathering of the parent material was partly induced by freeze–thaw processes associated with periglacial active layer development possibly during this period (Tye et al., 2012). Although proglacial glaciogenic deposits have been found in the vicinity of CW, the prevalence of similar deposits on the study hillslope has not been studied. However, unpublished work conducted by the authors suggests that the upper (3–5 m) of the lithosphere at both sites was subject to high-magnitude sediment transport at least 200 000 BP or before, potentially during the Anglian glaciation (∼450 000 BP). The complex land use and vegetation change in the Sherwood Sandstone outcrop, within which RFF is based, has been extensively studied and mapped by Tye et al. (2013). Following the onset of the Holocene, the area has been dominated by a complex sequence of land use change including broadleaf woodland (6000–2000 BCE), heathland (43–409 CE) and landscaped heathland for hunting (1600 CE). From at least 1855 CE, RFF has been under an arable regime and in the last 12 years, the dominant crops have been winter wheat and rye. CW is understood to have been an open field until 1903–1926 and then heathland until 1954. Between 1954 and the present day, however, the site has been continuously occupied by a coniferous forest (Mike Annis, personal communication, 8 October 2018).
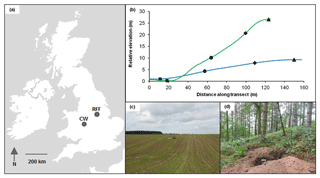
Figure 1Locations of the study sites in this paper (a) with elevation profiles (b) for both Comer Wood (CW; green) and Rufford Forest Farm (RFF; blue). The position of summit (triangles), shoulder (diamonds), backslope (circles) and toeslope (squares) sampling positions are indicated on each profile. Photographs of RFF (c) and CW (d) were taken by the author at the time of sampling.
2.2 Saprolite extraction and soil sampling
Four positions (summit, shoulder, backslope and toeslope) along a catena transect were selected for depth-to-bedrock surveys and saprolite extraction. First, a dynamic cone penetrometer was used to estimate the depth of the soil–saprolite interface. At RFF, a percussion drilling rig then proceeded to extract a series of vertical undisturbed core samples of the soil and saprolite. Cores were later halved lengthways, and by observing the changes in the consolidation and physical integrity of the extracted material (i.e. whether it remained intact when removed from the core), together with the penetration resistance data acquired in the field, the soil–saprolite interface was demarcated. Two samples of saprolite (5 cm thickness) were then subsampled for cosmogenic radionuclide analysis: one at this interface and one from 50 cm below. In CW, following the use of the dynamic cone penetrometer to locate suitable sites, a soil pit was manually dug vertically at each of the four sampling locations. Observing the changes in the consolidation and physical integrity of the material down the profile wall, together with the penetration resistance data, the soil–saprolite interface was ascertained. A sample of saprolite (5 cm thickness) was then extracted from this interface for cosmogenic isotope analysis.
The bombardment of quartz minerals in the uppermost metres of bedrock with cosmic rays leads to the production of 10Be. Assuming the intensity of these cosmic rays and the in situ weathering of bedrock (ε) is constant, the concentration of 10Be (N) in a sample of bedrock, as shown in Eq. (1), is dependent upon the balance of two factors: the time that the bedrock has been exposed to cosmic rays with longer durations leading to greater concentrations and the weathering of this bedrock into mobile regolith (soil) with greater rates of bedrock weathering leading to smaller concentrations (Lal, 1991; Stockmann et al., 2014). We assume here that the production of 10Be and the erosion of the bedrock is at an equilibrium:
where P is the annual production rates of 10Be by spallation, fast muons and stopping muons (sp, μf and μ−) at a surface with slope Θ; x is the mass sample depth (ρ⋅z); ρ is the density of overburden material; z is the depth of the sample; t is the age of the bedrock surface (the age when the original surface was generated; t is usually considered infinite); λ is the decay constant of 10Be with λ equalling In2 divided by the half-life of 10Be; and Λ is the mean attenuation of cosmic radiations (Lal, 1991). At RFF, we took two samples from the same depth profile at each catena position to test if the data support these assumptions. RFF data are compatible with landscape ages >200 ka. Production rates, decay constants and attenuation lengths were calculated using field data and the CRONUS-Earth online calculator v2.3 MATLAB code using Lal–Stone (St) scaling (Balco et al., 2008). As N can be measured using accelerator mass spectrometry (AMS), Eq. (1) can be solved for ε by simply interpolating N.
A total of 12 samples of saprolite (eight from RFF and four from CW) were prepared for AMS at the Cosmogenic Isotope Analysis Facility, East Kilbride, Scotland. This comprised mineral separation, quartz cleaning and procedures leading to the preparation of BeO sample cathodes (Kohl and Nishiizumi, 1992; Fifield, 1999; Corbett et al., 2016). The AMS measurements were carried out at the SUERC (Scottish Universities Environmental Research Centre) AMS laboratory (Xu et al., 2010). 10Be concentrations are based on a ratio of 10Be / 9Be as defined as the NIST Standard Reference Material 4325. The processed blank ratio ranged between 6 % and 13 % of the sample 10Be / 9Be ratios. The uncertainty of this correction is included in the stated standard uncertainties. Concentrations of 10Be were subsequently determined, following Balco (2006) (see Table S1 in the Supplement).
Previous work (e.g. Heimsath et al., 1997) has assumed that the bulk density of the soil above the bedrock surface is either equal to that of the bedrock or constant with depth. For this paper, we developed a model called “coSOILcal” to calculate soil formation rates using empirically measured bulk density data from each catena position at both RFF and CW. The local annual production rate of 10Be at each study site must also account for any obstructions that reduce the cosmic ray flux to the parent material (Phillips et al., 2016). For an obstruction to cause this reduction, it is required to be several metres thick which equates, in practice, to topographic features at the scale of tens of metres or greater. The shielding factor, therefore, is a ratio of the 10Be production rate at the obstructed site to that at an identical site but with a flat surface and a clear horizon (Balco et al., 2008). To calculate both shielding factors and subsequently normalize local 10Be production rates, site elevation, latitude and longitude were inputted into the CRONUS-Earth MATLAB code v2.3 using St scaling (Balco et al., 2008).
Soil samples were subsampled every 5 cm from each core at RFF and on each profile wall in CW. All samples were then oven dried overnight (105 ∘C for 12 h), grounded with a pestle and mortar, and sieved to discard the >2 mm fraction before being subject to particle size analysis and loss on ignition (LOI). Particle size analysis was conducted using a Beckman Coulter LS 13 320 Laser Diffraction Particle Size Analyser (pump speed: 70 %; sonication: 10 s; run length: 30 s). For LOI, 5 g of each sample was placed in a Carbolite furnace CWF 1300 (550 ∘C for 12 h).
The soils at RFF are classified as Arenosols (IUSS Working Group WRB, 2015) with weak horizonization. An Ap loamy-sand horizon (82 % sand, 16 % silt, 2 % clay) thickens from 30 to 75 cm and increases in LOI content from 3.65 % to 3.91 % from summit to toeslope, respectively. Despite being subject to arable practices for over 150 years, the presence of a 30 cm Ap horizon may be explained in part by the incorporation of mineral matter with the remaining organic material after harvest, although further isotopic work is required to verify this for RFF. This Ap horizon is underlain by a 5 cm fluvial pebble bed, typical of the Bunter Pebble Beds found in the vicinity (Ambrose et al., 2014). An undifferentiated, weakly consolidated subsoil steadily grades into saprolitic, moderately consolidated sandstone. The soils in CW are classified as Arenosols (IUSS Working Group WRB, 2015). Similar to RFF, there is little evidence for horizonization down the profile in CW. A thin (<5 cm) layer of litter fermentation and humus overlays an undifferentiated, weakly consolidated, sandy subsoil (94 % sand, 5 % silt, 1 % clay) and grades into moderately consolidated saprolitic sandstone. The sandy composition of these soils suggests that proglacial outwash deposits have not contributed to the soils of the study sites and that, instead, the soils are largely residual.
2.3 Lifespan analysis at Rufford Forest Farm
To provide an insight into the sustainability of the soil profiles at RFF under arable agriculture, in terms of the balance of erosion and formation, a first-order lifespan model was employed. Calculating the sustainability of a net-eroding soil in first-order terms has been attempted in the past (Elwell and Stocking, 1984; Sparovek and Schnug, 2001; Montgomery, 2007; Medeiros et al., 2016). Early models (Stocking and Pain, 1983), however, did not account for mass inputs into the soil system, such as that derived from bedrock weathering. In this study, this omission was addressed by using soil formation rates empirically measured at RFF. Furthermore, in previous models, the solum thickness used to calculate the soil lifespan is not universally consistent. Some authors constrain the lifespan by the minimum depth required for primary production (Stocking and Pain, 1983; Elwell and Stocking, 1984). Notwithstanding the fact that this soil threshold depth will, in part, be crop-dependent, soils that fall below this threshold may still be able to fulfil some of the ecosystem services, such as the sequestration of carbon. To address this here, two lifespan (L) scenarios were calculated, both of which are based on the continuation of contemporary arable agriculture. The first referred to the expected lifespan of the current A horizon (D=30 cm across the catena). At the toeslope, an additional lifespan was calculated to account for the greater depth (75 cm) of the A horizon. Here, we did not account for any transformation of subsoil into topsoil, which could occur if erosion rates are sufficiently low, nor did we account for any allochthonous inputs into the profile such as aeolian additions and organic amendments. The second estimated the time until the underlying parent material is exposed. Here, the observed depth to the soil–saprolite interface at each catena position was employed.
Both lifespan scenarios were calculated for summit, shoulder, backslope and toeslope catena positions. Three different erosion rates (E) were applied. First, a mean annual erosion rate of 1.19 mm yr−1 was used based on 137Cs-based data (n=103) measured by Quine and Walling (1991) at RFF. This mean value represents all erosion processes, including water-based and tillage-based erosion. Two additional lifespans were calculated using rates from the 5th and 95th percentiles of this dataset (0.19 and 2.2 mm yr−1, respectively). It should be acknowledged here that the rates of soil formation represent timescales 4 orders of magnitude greater than those of soil erosion. However, if lifespans are to provide an insight into the sustainability of the soil profiles at RFF, the soil erosion rates must represent those from contemporary arable agriculture.
The soil formation rates, as empirically measured in this paper, were then plotted to derive the soil production function P, such that
where W is the production rate at zero soil thickness (h) and γ is a parameter that determines the thickness of soil when soil formation falls off by 1∕e. The data for both the production rate (P) and the thickness of the soil (h) were used to calculate W and γ using least-squares regression. In this study, γ was calculated as being 2.26 m, which is substantially greater than previously reported values (e.g. Heimsath et al., 1997). It was therefore concluded that soil formation rates at RFF are relatively insensitive to changes in soil thickness. As a result, constant soil formation rates (F) for each catena position, together with two additional rates representing upper and lower standard deviations, were used to calculate soil lifespans. Furthermore, the expected increase in soil formation rates as a result of soil thinning was captured within these upper and lower uncertainties. Soil lifespans were thus calculated using
where D is the depth in millimetres, E is the gross annual soil erosion rate in millimetres per year and F is the gross annual soil formation rate in millimetres per year.
Table 110Be concentrations and calculated maximum soil formation rates for Rufford Forest Farm (RFF) and Comer Wood (CW).
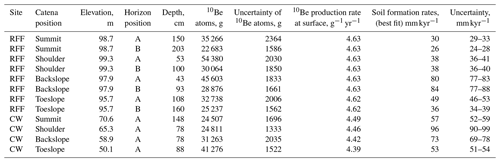
Horizon position A denotes the sample was taken at the soil–saprolite interface. Horizon position B denotes an additional sample was taken ∼50 cm below the interface
from the same depth profile. The depth here refers to that for the midpoint (between the top and bottom) of the sample. The shielding correction was calculated as 1.0 (to 1 d.p., decimal point)
for all samples, and 10Be production rates are corrected for elevation and location (see Table S1 in the Supplement). All uncertainties are 1 standard deviation and are
based on uncertainties in the measurement of 10Be concentration as outlined in Rodés et al. (2011).
3.1 Soil formation rates
Soil formation rates calculated from measured 10Be concentrations at RFF range from 0.026 to 0.084 mm yr−1, with the mean soil formation rate being 0.048±0.008 mm yr−1 (Table 1). In CW, soil formation rates range from 0.053 to 0.096 mm yr−1, with the mean soil formation rate being 0.070±0.010 mm yr−1, which is 0.022 mm yr−1 greater than that at RFF. These rates indicate declining soil formation rates with increasing soil thickness (Figs. 2–3). In accordance with geomorphological theory (Conacher and Dalrymple, 1977; King et al., 1983; Pennock, 2003; Schaetzl, 2013), soils are thinner on the slope convexities and the steepest gradients, where surface erosion is considered most prevalent. In contrast, soil thicknesses are greater at the summit, where surface erosion has been less extensive, and the toeslope zone, where sediment is deposited. At RFF, the fastest soil formation rates were found on the backslope where soils are thinnest. These results are consistent with many theorized mechanisms that demonstrate how parent material overlain by shallower soils is more affected by diurnal thermal stresses, contact with water and physical disturbance which can together proliferate physical and chemical weathering processes and thus the conversion of saprolite into soil. Conversely, it was found the slowest formation rates were associated with the deepest soils at the summit where the increasing thickness of the soil mantle buffers the parent material from any subaerial factors that may otherwise proliferate weathering (Carson and Kirkby, 1972; Cox, 1980; Dietrich et al., 1995; Minasny and McBratney, 1999; Wilkinson and Humphreys, 2005). In CW, the difference in soil thickness between eroding and non-eroding zones is less pronounced. On the shoulder and backslope positions, where soils are thinnest, the soil formation rates were 0.03 mm yr−1 faster than summit and toeslope positions.
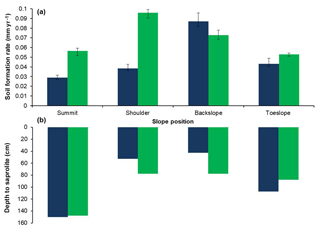
Figure 2Soil formation rates and the depths to saprolite for the four sampling positions along the catena transects at Rufford Forest Farm (blue; n=4) and Comer Wood (green; n=4). The error bars represent 1σ uncertainties. At RFF, two 10Be concentrations down the same depth profile have been used in the coSOILcal model to derive a “best fit” soil formation rate. Depth here refers to that for the midpoint (between the top and bottom) of the sample.
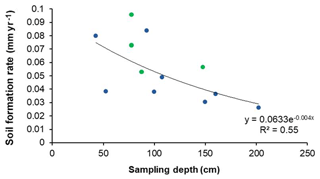
Figure 3Soil formation rates against sampling depth for Rufford Forest Farm (blue; n=8) and Comer Wood (green; n=4). Depth here refers to that for the midpoint (between the top and bottom) of the sample.
Comparing data between RFF and CW demonstrates that there are other factors besides soil thickness that govern soil formation rates. For example, at the shoulder the soil thickness in CW is greater by 25 cm than that at RFF, which would suggest slower formation rates. Instead soil formation rates are faster by 0.038 mm yr−1 in CW. One possible explanation is the petrographic composition of the parent material and the susceptibility of that parent material to weathering. Whilst both RFF and CW are underlain by sandstone, the bedrock at RFF is fluvially derived whereas that in CW is aeolian-derived. Petrological studies on fluvially derived sandstone report a greater concentration of cementing clays in the matrix material which ultimately reduces the porosity and decreases its susceptibility to particle detachment, leading to slower soil formation rates (Wakatsuki et al., 2005; Mareschal et al., 2015).
In studies where cosmogenic methodologies have not been applied, it has been found that land use regime can promote or retard rates of bedrock weathering. Humphreys (1994) found that root channels and mesofaunal pedotubles in both the topsoil and subsoil can enhance the surface-to-bedrock hydrological connectivity. Similarly, Dong et al. (2019) demonstrated how an interconnected network of ecohydrologic interactions controls the supply and transport of acid to the bedrock. When a greater proportion of root mass was distributed in the uppermost horizons of the soil profile, CO2 was predominantly emitted as gas, whereas when roots were distributed in the subsoil, more CO2 moved downwards to increase acid production and enhance chemical weathering. Other work has sought to identify the mechanisms that affect the thermal regime of soil profiles and the consequential impacts on the weathering susceptibility of the parent material (Ahnert, 1967; Minasny and McBratney, 1999). In CW, the roots are deeper than those observed at RFF, and this is likely to proliferate weathering processes. However, given the fact that the 10Be-derived soil formation rates are millennial-scale averages, it is unlikely that relatively recent (decadal–centennial) variances in the site's land use regime would be captured in the isotopic data (Darvill et al., 2013).
3.2 Derived soil formation rates in reference to the global inventory
Figure 4 compares soil formation rates for the study sites to an inventory of soil formation rates extracted from the published literature (n=252; Fig. 4a; Table S2 in the Supplement). The median soil formation rate in this study (0.051 mm yr−1) is 0.028 mm yr−1 faster than that of the mantled inventory, a statistically significant difference (U test; P<0.05). However, this global inventory comprises studies conducted on a range of geologies and climates, which are both influences on bedrock weathering rates.
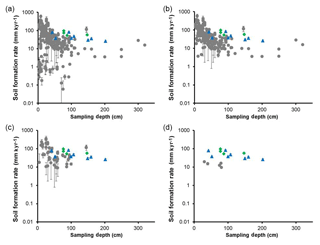
Figure 4Soil formation rates from a globally compiled inventory (grey circles) and from this study at Rufford Forest Farm (blue triangles) and Comer Wood (green diamonds) plotted against sampling depth. The depth here refers to that for the midpoint (between the top and bottom) of the sample. Rates in grey are from (a) the total mantled inventory (n=252); (b) studies from temperate climates (n=187); (c) studies on sandstone geology (n=57); and (d) the UK, exclusively from Riggins et al. (2011) (n=5). Error bars indicate the standard error.
Isolating the data from temperate climates (n=187; Fig. 4b) presents a median soil formation rate of 0.035 mm yr−1, which is 0.016 mm yr−1 slower than that measured for RFF and CW, although there is no statistically significant difference between those data and those we have measured at the UK study sites presented in this paper (U test; P>0.05). It is likely that the inventory's median soil formation rate for temperate climates is slower as 44 % of the temperate-based data have been collected from regions that have lower mean annual precipitation than RFF and CW which can lead to less weathering activity at the parent material (Heimsath et al., 2001, 2005, 2012; Dixon et al., 2009).
Isolating the sandstone-derived data from the inventory (n=57; Fig. 4c) presents a median soil formation rate of 0.045 mm yr−1 which is 0.006 mm yr−1 slower than that measured for RFF and CW, although there is no statistically significant difference (U test; P>0.05). Although the sandstone-derived data were derived from the global soil-mantled database, all data stem from sites in temperate climates which reduces the influence that climate may have otherwise had in this analysis on lithology. We suggest that faster formation rates at RFF and CW may be explained by the fact that the specific varieties of sandstone at these study sites are generally more susceptible to weathering than those within the sandstone-based inventory. Of those sandstone varieties, the dominant form is the greywacke, which is characterized by a hard, fine-grained argillaceous matrix and which has a greater resistance to weathering than others (Cummins, 1962). Although there has been substantial work on the susceptibilities of major geological rock types to weathering (Stockmann et al., 2014; Wilson et al., 2017), we do not know of any study which seeks to identify whether the susceptibility of specific varieties of sandstone have an influence on soil formation rates.
The only other study to measure soil formation rates in the UK is that of Riggins et al. (2011), where rates were derived for Bodmin Moor, Cornwall (n=5; Fig. 4d). In that study, the median soil formation rate was 0.015 mm yr−1, which is 0.036 mm yr−1 slower than that for RFF and CW and is statistically significant (U test; P<0.05), despite the fact that Bodmin Moor receives about 300 mm more precipitation per year than the sites in this study, which should increase soil formation rates (Riggins et al., 2011). This is explained by the parent material at Bodmin Moor (coarse-grained granite) being generally less prone to weathering than the varieties of sandstone at RFF and in CW (Portenga and Bierman, 2011).
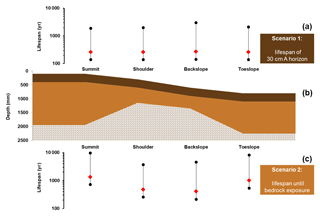
Figure 5First-order soil lifespans calculated at four catena positions at Rufford Forest Farm for Scenario 1 (the time until the erosion of a 30 cm A horizon) and Scenario 2 (the time until bedrock exposure). Panel (b) indicates the thickness of the A horizon (dark brown), the subsoil (light brown) and the depth to the soil–saprolite interface (bricks). Red diamonds denote lifespans calculated using a mean annual soil erosion rate of 1.19 mm yr−1 from Quine and Walling (1991) and soil formation rates from this study. Black dots denote the minimum and maximum lifespans calculated using the 5th and 95th percentile of the soil erosion dataset and the 1σ uncertainties in the soil formation dataset.
3.3 Lifespan analysis at Rufford Forest Farm
Based on a mean annual erosion rate of 1.19 mm yr−1 under arable agriculture, the lifespans of the A horizon across the catena at RFF range between 258 and 272 years (Fig. 5). This range expands to 138–3000 years when the 5th and 95th percentile soil erosion rates are applied. However, further examination of the A horizon from cores extracted down the catena suggest that the toeslope is in a phase of aggradation rather than thinning. This is supported by the fact that the depth of the Ap horizon at the toeslope is 75 cm, whereas it is 30 cm on all other observed landscape positions. Moreover, comprised within the upper stratigraphy of the soil profile down the catena is the Bunter Pebble Bed which can be found at approximately 30 cm on summit, shoulder and backslope positions but 70 cm at the toeslope. The depth to which this pebble bed occurs at the toeslope suggests that either colluviation has occurred or is still occurring. In a scenario where colluviation is no longer active, the lifespan of this 75 cm A horizon is finite and ranges from 347 to 5245 years, but lifespans here could be longer or indefinite if colluviation continues. This demonstrates the difficulty of calculating lifespans using soil formation rates derived from bedrock alone and not from other system inflows of soil mass such as that from colluviation and soil carbon additions.
Soil lifespans indicating the time until the exposure of the parent material span between 407 and 1334 years. The range of these lifespans can be explained by the fact that unlike scenario one, where a constant A horizon thickness of 30 cm was applied across the catena, the soil thickness applied here is the depth to the soil–saprolite interface measured at each catena position (see Table 1). Applying upper and lower confidence intervals in the soil formation term and the 5th and 95th percentiles in the soil erosion term further widens the breadth of lifespans to 212–9688 years. The shortest lifespans are found on the backslope where bedrock exposure is expected to occur between 212 and 4500 years. In contrast, the greatest lifespans are found at the summit where soil thickness is 155 cm (713–9688 years). Although soil formation rates are greater at the toeslope, the depth to bedrock is 40 cm greater at the summit, and, as a result, longer durations are required for bedrock to become exposed at this position. The soil detached and transported from the backslope is expected, in part, to continue to be a contributory source of the colluvium observed at the toeslope. Although the growth of soil profiles due to colluvium is not considered in the lifespan equation, it suggests that lifespans at the toeslope may either be longer than the calculated maximum of 8042 years or indefinite.
The first-order lifespans presented here are based on a number of assumptions. Notwithstanding the fact that the land management regime may change within the cited time spans, altering the protection the soils receive from wind and water, the erosion rates employed reflect neither the increase in the erodibility of subsoil horizons, characterized by a relatively weaker soil structure (Tanner et al., 2018), nor the potential role that the Bunter Pebble Bed may play in armouring the soil surface in the future. Moreover, they do not reflect the expected shift in erosivity, commensurate with more intense precipitation events (Burt et al., 2015). Acknowledging these factors, the lifespans presented here are likely to be overestimated. However, the fate of eroded soil upslope may contribute to the build-up of soil profiles in downslope concavities, extending the lifespans in the colluvial zone. In this respect the lifespans presented here, particularly those for the toeslope, are likely to be underestimated.
We have presented the first isotopically derived rates of soil formation for soils currently supporting arable agriculture. Rates derived for two UK catena sequences using cosmogenic radionuclide analysis range from 0.026 to 0.096 mm yr−1, with mean rates being 0.048±0.008 and 0.070±0.010 mm yr−1 for Rufford Forest Farm and Comer Wood, respectively. By combining soil formation rates from Rufford Forest Farm with soil erosion rates derived from a prior isotopic study in a first-order lifespan model, we estimate that in a worst-case scenario the soil that currently comprises the A horizon on the backslope may be eroded in 138 years and bedrock exposure may occur in 212 years. Assessing gross soil erosion with measured rates of soil formation is important because soils that support arable agriculture are under threat from accelerated soil erosion. We have therefore shown that both the derivation and application of soil formation rates must become a fundamental component in future discussions of soil sustainability.
This work also represents the second of all isotopic studies of soil formation in the UK and therefore a significant contribution to our knowledge of pedogenesis. Soil formation rates were found to fall within the range of those previously published for soils in temperate climates and on sandstone lithologies, but they were found to be significantly greater than those measured previously at Bodmin Moor. This is explained by the fact that the parent material at Bodmin Moor is a coarse-grained granite and therefore less susceptible to weathering than the sandstone materials underlying Rufford Forest Farm and Comer Wood. Such petrographic controls may also explain the greater rates of soil formation in Comer Wood, where the sandstone matrix is largely devoid of the cementing agents present at Rufford Forest Farm, and, therefore, where it is more susceptible to particle detachment during physical and chemical weathering. Given that petrographic variability has not been thoroughly investigated in pedogenesis work, greater investment is warranted to better understand how the geochemical composition of the parent material governs the rates of soil formation.
All related data can be found in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/soil-5-253-2019-supplement.
DLE, JNQ, AMT and JACD designed the research. DLE and AMT conducted sampling. DLE and AR conducted laboratory work and analysed results. DLE prepared the paper with contributions from all co-authors.
John N. Quinton is a member of the editorial board of the journal.
The authors wish to thank Mike Annis (National Trust) for permission to carry out fieldwork on Comer Wood and Tom and Kathy King (TAG Farming) for permission to carry out fieldwork on Rufford Forest Farm. We thank Vassil Karloukovski for assistance in surveying and Andrew Binley, Paul McLachlan, Jonathan Riley, Carl Horabin and the BGS Dando Drilling Rig Team for the acquisition of samples. We also wish to thank Allan Davidson, Ángel Rodés, Derek Fabel at the NERC Cosmogenic Isotope Analysis Facility for preparing samples for AMS and their subsequent assistance in data analysis. We thank Timothy A. Quine for sharing multiple datasets from fieldwork conducted at Rufford Forest Farm. Finally, we wish to thank the anonymous referees and Daniel Morgan for their very constructive feedback on the paper.
This work was partly supported by BBSRC and NERC through a Soils Training and Research Studentships (STARS) grant (no. NE/M009106/1) and partly by a NERC research grant (no. CIAF 9179/1017). STARS is a consortium consisting of Bangor University, the British Geological Survey, the Centre for Ecology and Hydrology, Cranfield University, the James Hutton Institute, Lancaster University, Rothamsted Research and the University of Nottingham.
This paper was edited by Peter Finke and reviewed by Daniel Morgan and two anonymous referees.
Ackerer, J., Chabaux, F., Van der Woerd, J., Viville, D., Pelt, E., Kali, E., Lerouge, C., Ackerer, P., di Chiara Roupert, R., and Négrel, P.: Regolith evolution on the millennial timescale from combined U-Th-Ra isotopes and in situ cosmogenic 10Be analysis in a weathering profile (Strengbach catchment, France), Earth Planet. Sc. Lett., 453, 33–43, 2016.
Ahnert, F.: The role of the equilibrium concept in the interpretation of landforms of fluvial erosion and deposition, in: L'evolution des versants, edited by: Macar, P., Universite de Liege, Liege, pp. 23–41, 1967.
Alexander, E. B.: Rates of Soil Formation: Implications for Soil-Loss Tolerance, Soil Sci., 145, 37–45, 1988.
Ambrose, K., Hough, E., and Smith, N. J. P.: Lithostratigraphy of the Sherwood Sandstone Group of England, Wales and south-west Scotland, available at: http://nora.nerc.ac.uk/id/eprint/507530 (last access: 30 September 2018), 2014.
Amundson, R., Berhe, A. A., Hopmans, J. W., Olson, C., Sztein, A. E., and Sparks, D. L.: Soil and human security in the 21st century, Science, 348, 1261071, https://doi.org/10.1126/science.1261071, 2015.
Balco, G.: Converting Al and Be isotope ratio measurements to nuclide concentrations in quartz, available at: http://hess.ess.washington.edu/math/docs/common/ams_data_reduction/ (last access: 30 September 2018), 2006.
Balco, G., Stone, J. O., Lifton, N. A., and Dunai, T. J.: A complete and easily accessible means of calculating surface exposure ages or erosion rates from 10Be and 26Al measurements, Quat. Geochronol., 3, 174–195, 2008.
Borrelli, P., Robinson, D. A., Fleischer, L. R., Lugato, E., Ballabio, C., Alewell, C., Meusburger, K., Modugno, S., Schütt, B., Ferro, V., Bagarello, V., Van Oost, K., Montanarella, L., and Panagos, P.: An assessment of the global impact of 21st century land use change on soil erosion, Nature Comm., 8, 1–13, 2017.
Bryan, W. H. and Teakle, L. J. H.: Pedogenic Inertia: a Concept in Soil Science, Nature, 164, 969, 1949.
Burke, B. C., Heimsath, A., and White, A. F.: Coupling chemical weathering with soil production across soil-mantled landscapes, Earth Surf. Proc. Land., 32, 853–873, 2007.
Burt, T., Boardman, J., Foster, I., and Howden, N.: More rain, less soil: long-term changes in rainfall intensity with climate change, Earth Surf. Proc. Land., 41, 563–566, 2015.
Carson, M. A. and Kirkby, M. J.: Hillslope form and process, Cambridge University Press, Cambridge, 1972.
Conacher, A. J. and Dalrymple, J. B.: The nine unit landsurface model: an approach to pedogeomorphic research, Geoderma, 18, 3–154, 1977.
Corbett, L. B., Bierman, P., and Rood, D. H.: An approach for optimizing in situ cosmogenic 10Be sample preparation, Quat. Geochronol., 33, 24–34, 2016.
Cox, N. J.: On the relationship between bedrock lowering and regolith thickness, Earth Surf. Proc., 5, 271–274, 1980.
Cummins, W. A.: The Greywacke problem, Geol. J., 3, 51–72, 1962.
Darvill, C. M.: Cosmogenic nuclide analysis, in: Geomorphological Techniques, edited by: Clarke, L., British Society for Geomorphology, London, ch. 4, sec. 2.10, 2013.
Dietrich, W. E., Reiss, R., Hsu, M., and Montgomery, D. R.: A process-based model for colluvial soil depth and shallow landsliding using digital elevation data, Hydrol. Process., 9, 383–400, 1995.
Dixon, J. I., Heimsath, A. M., and Amundson, R.: The critical role of climate and saprolite weathering in landscape evolution, Earth Surf. Proc. Land., 34, 1507–1521, 2009.
Dokuchaev, V. V.: Mapping the Russian Soils, Imperial University of St. Petersburg, Russia, 1879.
Dong, X., Cohen, M. J., Martin, J. B., McLaughlin, D. L., Murray, A. B., Ward, N. D., Flint, M. K., and Heffernan, J. B.: Ecohydrologic processes and soil thickness feedbacks control limestone-weathering rates in a Karst landscape, Chem. Geol., in press, 2019.
Elwell, H. A. and Stocking, M. A.: Estimating soil life-span for conservation planning, Trop. Agr., 61, 148–150, 1984.
FAO and ITPS: Status of the World's Soil Resources (SWSR) Main Report, Food and Agriculture Organisation of the United Nations and Intergovernmental Technical Panel on Soils, Rome, Italy, 2015.
Fifield, L. K.: Accelerator mass spectrometry and its application, Reports on Progress in Physics, 62, 1223–1274, 1999.
Gosse, J. C. and Phillips, F. M.: Terrestrial in situ cosmogenic nuclides: theory and application, Quaternary Sci. Rev., 20, 1475–1560, 2001.
Govers, G., Quine, T. A., Desmet, P. J. J., and Walling, D. E.: The relative contribution of soil tillage and overland flow erosion to soil redistribution on agricultural land, Earth Surf. Proc. Land., 21, 929–946, 1996.
Govers, G., Merckx, R., van Wesemael, B., and Van Oost, K.: Soil conservation in the 21st century: why we need smart agricultural intensification, SOIL, 3, 45–59, https://doi.org/10.5194/soil-3-45-2017, 2017.
Hancock, G. R., Wells, T., Martinez, C., and Dever, C.: Soil erosion and tolerable soil loss: insights into erosion rates for a well-managed grassland catchments, Geoderma, 237, 256–265, 2015.
Heimsath, A. M.: Eroding the land: steady-state and stochastic rates and processes through a cosmogenic lens, Geological Society of America, 415, 111–129, 2006.
Heimsath, A. M.: Limits of Soil Production?, Science, 343, 617–618, 2014.
Heimsath, A. M. and Burke, B. C.: The impact of local geochemical variability on quantifying hillslope soil production and chemical weathering, Geomorphology, 200, 75–88, 2013.
Heimsath, A. M., Dietrich, W. E., Nishiizumi, K., and Finkal, R. C.: The Soil Production Function and Landscape Equilibrium, Nature, 388, 358–361, 1997.
Heimsath, A. M., Dietrich, W. E., Nishiizumi, K., and Finkel, R. C.: Stochastic processes of soil production and transport: erosion rates, topographic variation and cosmogenic nuclides in the Oregon Coast Range, Earth Surf. Proc. Land., 26, 531–532, 2001.
Heimsath, A. M., Furbish, D. J., and Dietrich, W. E.: The illusion of diffusion: field evidence for depth-dependent sediment transport, Geology, 33, 949–952, 2005.
Heimsath, A. M., DiBiase, R. A., and Whipple, K. X.: Soil production limits and the transition to bedrock-dominated landscapes, Nat. Geosci., 5, 210–214, 2012.
Humphreys, G. S.: Bioturbation, biofabrics and the biomantle: an example from the Sydney Basin, in: Soil Micromorphology: studies in management and genesis, edited by: Ringrose-Voase, A. J. and Humphreys, G. S., Elsevier, Amsterdam, pp. 421–436, 1994.
IUSS Working Group WRB: World Reference Base for Soil Resources 2014, update 2015 International soil classification system for naming soils and creating legends for soil maps, World Soil Resources Reports No. 106, FAO, Rome, 2015.
Jenny, H.: Factors of Soil Formation: A System of Quantitative Pedology, McGraw-Hill, New York, 1941.
King, G. J., Acton, D. F., and St. Arnaud, R. J.: Soil-landscape analysis in relation to soil redistribution and mapping at a site within the Weyburn association, Can. J. Soil Sci., 63, 657–670, 1983.
Kohl, C. P. and Nishiizumi, K.: Chemical isolation of quartz for measurement of in-situ produced cosmogenic nuclides, Geochim. Cosmochim. Ac., 56, 3583–3587, 1992.
Lal, D.: Cosmic ray labelling of erosion surfaces: in situ nuclide production rates and erosion models , Earth Planet. Sc. Lett., 104, 424–439, 1991.
Mareschal, L., Turpault, M. P., and Ranger, J.: Effect of granite crystal grain size on soil properties and pedogenic processes along a lithosequence, Geoderma, 249, 12–20, 2015.
Medeiros, G. O. R., Giarolla, A., Sampalo, G., and Marinho, M. A.: Diagnosis of the Accelerated Soil Erosion in São Paulo State (Brazil) by the Soil Lifetime Index Methodology, Revista Brasileira de Ciência do Solo, 40, 1–15, 2016.
Met Office: HadUK-Grid gridded and regional average climate observations for the UK, available at: http://catalogue.ceda.ac.uk/uuid/4dc8450d889a491ebb20e724debe2dfb (last access: 31 August 2019), 2018.
Minasny, B. and McBratney, A. B.: A rudimentary mechanistic model for soil production and landscape development, Geoderma, 90, 3–21, 1999.
Minasny, B., Finke, P., Stockmann, U., Vanwalleghem, T., and Bratney, A. B.: Resolving the integral connection between pedogenesis and landscape evolution, Earth-Sci. Rev., 150, 102–120, 2015.
Montgomery, D. R.: Soil erosion and agricultural sustainability, P. Natl. Acad. Sci. USA, 104, 13268–13272, 2007.
Panagos, P., Imeson, A., Meusburger, K., Borrelli, P., Poesen, J., and Alewell, C.: Soil conservation in Europe: Wish or Reality?, Land Degradation and Development, 27, 1547–1551, 2016.
Pennock, D. J.: Terrain attributes, landform segmentation, and soil redistribution, Soil Tillage Research, 69, 15–26, 2003.
Phillips, J. D.: The convenient fiction of steady-state soil thickness, Geoderma, 156, 389–398, 2010.
Phillips, F. M., Argento, D. C., Balco, G., Caffee, M. W., Clem, J., Dunai, T. J., Finkel, R., Goehring, B., Gosse, J. C., Hudson, A. M., Jull, A. J. T., Kelly, M. A., Kurz, M., Lal, D., Lifton, N., Marrero, S. M., Nishiizumi, K., Reedy, R. C., Schaefer, J., Stone, J. O. H., Swanson, T., and Zreda, M. G.: The CRONUS-Earth Project: A synthesis, Quat. Geochronol., 31, 119–154, 2016.
Pimentel, D., Harvey, C., Resosudarmo, P., Sinclair, K., Kurz, D., McNair, M., Crist, S., Shpritz, L., Fitton, L., Saffouri, R., and Blair, R.: Environmental and Economic Costs of Soil Erosion and Conservation Benefits, Science, 267, 1117–1123, 1995.
Portenga, E. W. and Bierman, P. R.: Understanding Earth's eroding surface with 10Be, GSA Today, 21, 4–10, 2011.
Quine, T. A. and Walling, D. E.: Rates of soil erosion on arable fields in Britain: quantitative data from caesium-137 measurements, Soil Use Manage., 7, 169–176, 1991.
Quinton, J. N., Govers, G., Van Oost, K., and Bardgett, R. D.: The impact of agricultural soil erosion on biogeochemical cycling, Nat. Geosci., 3, 311–314, 2010.
Riggins, S. G., Anderson, R. S., Anderson, S. P., and Tye, A. M.: Solving a conundrum of a steady-state hilltop with variable soil depths and production rates, Bodmin Moor, UK, Geomorphology, 128, 73–84, 2011.
Rodés, Á., Pallàs, R., Braucher, R., Moreno, X., Masana, E., and Bourlés, D. L.: Effect of density uncertainties in cosmogenic 10Be depth-profiles: Dating a cemented Pleistocene alluvial fan (Carboneras Fault, SE Iberia), Quat. Geochronol., 6, 186–194, 2011.
Schaetzl, R. J.: Catenas and Soils, in: Treatise on Geomorphology, edited by: Shroder, J. F., Academic Press, San Diego, California, pp. 145–158, 2013.
Sparovek, G. and Schnug, E.: Temporal Erosion-Induced Soil Degradation and Yield Loss, Soil Sci. Soc. Am. J., 65, 1479–1486, 2001.
Stocking, M. A. and Pain, A.: Soil Life and the Minimum Soil Depth for Productive Yields: Developing a New Concept, University of East Anglia, School of Development Studies, Norwich, 1983.
Stockmann, U., Minasny, B., and McBratney, A. B.: How fast does soil grow?, Geoderma, 216, 48–61, 2014.
Struck, M., Jansen, J. D., Fujioka, T., Codilean, A. T., Fink, D., Egholm, D. L., Fülöp, R., Wilcken, K. M., and Kotevski, S.: Soil production and transport on postorogenic desert hillslopes quantified with 10Be and 26Al, GSA Bulletin, 130, 1017–1040, 2018.
Tanner, S., Katra, I., Argaman, E., and Ben-Hur, M.: Erodibility of waste (Loess) soils from construction sites under water and wind erosional forces, Sci. Total Environ., 616, 1524–1532, 2018.
Tugel, A. J., Herrick, J. E., Brown, J. R., Mausbach, M. J., Puckett, W., and Hipple, K.: Soil change, soil survey and natural resources decision making: a blueprint for action, Soil Sci. Soc. Am. J., 69, 738–747, 2005.
Turner, B. L., Hayes, P. E., and Laliberté, E.: A climosequence of chronosequences in southwestern Australia, Eur. J. Soil Sci., 69, 69–86, 2018.
Tye, A. M., Kemp, S. J., Lark, R. M., and Milodowski, A. E.: The role of peri-glacial active layer development in determining soil-regolith thickness across a Triassic sandstone outcrop in the UK, Earth Surf. Proc. Land., 37, 971–983, 2012.
Tye, A. M., Robinson, D. A., and Lark, R. M.: Gradual and anthropogenic soil change for fertility and carbon on marginal sandy soils, Geoderma, 207, 35–48, 2013.
UNCCD: Global Land Outlook, available at: https://knowledge.unccd.int/publication/full-report (last access: 31 August 2019), 2017.
Wakatsuki, T., Tanaka, Y., and Matsukura, Y.: Soil slips on weathering-limited slopes underlain by coarse-grained granite or fine-grained gneiss near Seoul, Republic of Korea, Catena, 60, 181–203, 2005.
Walling, D. E. and Quine, T. A.: The use of 137Cs measurements to investigate soil erosion on arable fields in the UK: potential applications and limitations, J. Soil Sci., 42, 147–165, 1991.
Wilkinson, M. T. and Humphreys, G. S.: Exploring pedogenesis via nuclide-based soil production rates and OSL-based bioturbation rates, Aust. J. Soil Res., 43, 767–779, 2005.
Wilkinson, M. T., Chappell, J., Humphreys, G. S., Fifield, K., Smith, B., Hesse, P., Heimsath, A. M., and Ehlers, T. A.: Soil production in heath and forest, Blue Mountains, Australia: influence of lithology and palaeoclimate, Earth Surf. Proc. Land., 30, 923–934, 2005.
Wilson, S. G., Lambert, J., Nanzyo, M., and Dahlgren, R. A.: Soil genesis and mineralogy across a volcanic lithosequence, Geoderma, 285, 301–312, 2017.
Xu, S., Dougans, A. B., Freeman, S., Schnabel, C., and Wilcken, K. M.: Improved Be-10 and Al-26 AMS with a 5 MV spectrometer, in: Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, Eleventh International Conference on Accelerator Mass Spectrometry, Rome, Italy, 14–19 September 2008, 736–738, 2010.
Zhao, T., Liu, W., Xu, Z., Liu, T., Xu, S., Cui, L., and Shi, C.: Cosmogenic nuclides (10Be and 26Al) erosion rate constraints in the Badain Jaran Desert, northwest China: implications for surface erosion mechanisms and landform evolution, Geosci. J., 23, 1–10, https://doi.org/10.1007/s12303-018-0010-7, 2018.





